introduction

Background & Motivation

  1. vBS (virtualized Base Station) 소개
    O-RAN architecure에서 RAN은 가상화된 네트워크 모듈을 기반(microservice)으로 구축됨. 이에 대한 결과로 vRAN이 형성되며, vBS가 중심 구성 요소임. 이 vBS는 CTO server에 호스팅할 수 있으며, 이는 OPEX(운영비)와 CAPEX(자본비)를 크게 절감할 수 있음.

  2. vBS 장점
    vBS에 프로그래밍이 가능해지면서, 기존의 고정적인 RAN 시스템에 성능 향상과 유연성을 가져다 줄 수 있을 것으로 예상됨.

  3. vBS 단점 - [4], [5], [6]
    에너지 소비가 불안정함. (less predictable performance)
    성능 예측이 어려움. (volatile energy consumption)
    특히 범용 컴퓨팅 인프라에 사용할 때 더욱 심해짐. (general-purpose computing)
    -> vBS operation, schedule 하는 방법을 이해해야함.

  4. 초기연구 : on learning vBS meta-policies - [7], [8]
    비실시간 규모에서 결정 후 각 vBS의 실시간 scheduler에 적용하는 규칙.
    O-RAN에서도 이와 같이 2 단계의 scheduling 내용이 있음.

    하지만 O-RAN에서 제안한 이론적 내용은 vBS의 전체 운영 프로필, 데이터 트래픽 예측, 채널 상태와 같은 정보를 알고 있다고 가정했기 때문에 실제 결과와의 차이가 매우 많이남. 실제에서는 실시간으로 정확히 파악할 수 없는 정보에 의존하지 않도록 규칙을 작성해야함.

  5. 본 논문 : vBS scheduling —(modeling)—> bandit learning problem
    다음과 같은 정보를 몰라도 효과적으로 meta-policy을 찾는 algorithm을 제안!
    (vBS operation, their hosting platforms, network conditions and data traffic, user needs)
    optimality criterion : user traffic -> effective throuput + energy consumption

  6. 참고 : meta-policy란?
    강화학습에서 policy(정책)을 학습하는 방법을 학습하는 접근 방식임. 일반적인 강화학습에서는 1개의 policy를 학습하지만, meta-policy 학습에서는 상황에 맞는 여러 policy를 선택하고 조정하는 meta-policy(상위 policy)를 학습함. 이 방식은 다양한 환경, 변화하는 상황에서 매우 유용함.

  1. softwarized networks에서 resource management를 optimization 방법
    · model based(modeling : control parameter - performance function)
    · model-free
    · Reinforcement Learning

  2. Model based - [4], [5], [10]
    vBS computing 용량 안에서 처리 가능한 traffic 최대화에 사용됨.
    but, vBS의 operation은 hosting platform과 network condition에 영향 받기 때문에 이들을 현실에서 사용하기 어려움.

  3. Model free - [11], [12], [13]
    Neural network를 사용해 performance function을 근사하여 network slicing, edge computing 등에서 활용.
    but, 학습 데이터의 유무가 크게 좌우됨.

  4. RL - [14], [15]
    실시간(runtime) 관측치를 활용하는 방법으로, interference management, SDN controllers에서 사용됨.
    but, curse of dimensionality(차원의 저주) 문제로 인해 성능 보장이 어려움.

  5. contextual bandit algorithm - [16], [17], [18], [19]
    video streaming rates, BS handover thresholds, assign CPU time to virtualized BSs, control mmWave networks 등에 사용됨
    but, performance function을 결정하는 context-related info(network conditions, traffic)이 필요

  6. 언급한 방법들의 한계
    network condition과 다른 시스템의 변동이 시간이 지나도 일정하게 유지되야한다는 가정이 필요하기 때문에 이러한 방법들은 heterogeneous and small-cell networks에서는 사용하기 힘듦.

  7. 본 논문
    위의 한계들을 피하기 위해 Exp3 algorithm을 기반으로 vBS control scheme을 개발함.
    · 견고한 성능 보장
    · 다양한 network 및 load 변동에 대응 가능
    · vBS의 performance function에 의존 x
    · 구현 단순 (무거운 행렬 계산을 요구하는 Bayseian 접근 방법과 다름 - [21])
    · adversarial bandit learning 방식 - [22], [23]

Contributions

이 논문에서는 vBS의 주요 작동 parameter에 대한 threshold를 결정하는 learning algorithm을 설계했음. parameter에는 vBS transmission power, eligible Modulation and Coding Scheme(MCS), duty cycle(or airtime)이 있음.

이 paramter들은 policy에 의해 조정되는데, policy는 실시간으로 업데이트되고, 이후 real-time scheduler에 전달되어 vBS parameter를 fine-tune함. 이렇게 vBS parameter를 직접 고정하지 않고 policy를 결정하는 방법을 meta-learning method라고 하는데, O-RAN architecure에서 중요한 요소이다. - [6], [18]

또한, 제안된 algorithm은 bandit feedback에 기반하며, assumption이나 information을 요구하지 않기 때문에, 다양한 유형의 vBS, hosting platform, network/traffic condition에서 실제 적용이 가능함.

.
.
.

SYSTEM MODEL AND PROBLEM STATEMENT

SYSTEM MODEL

· O-RAN 기반 : learning-based resource management가 포함됨 - [1], [7], [8]
· BBU(eNodeB/gNB(CU+DU)) + RU
· 목적 : vBS의 동작을 관리하는 policy를 설계하여 네트워크 상황 및 사용자 요구에 적응하며 성능과 에너지 사용을 최적화.

architecture

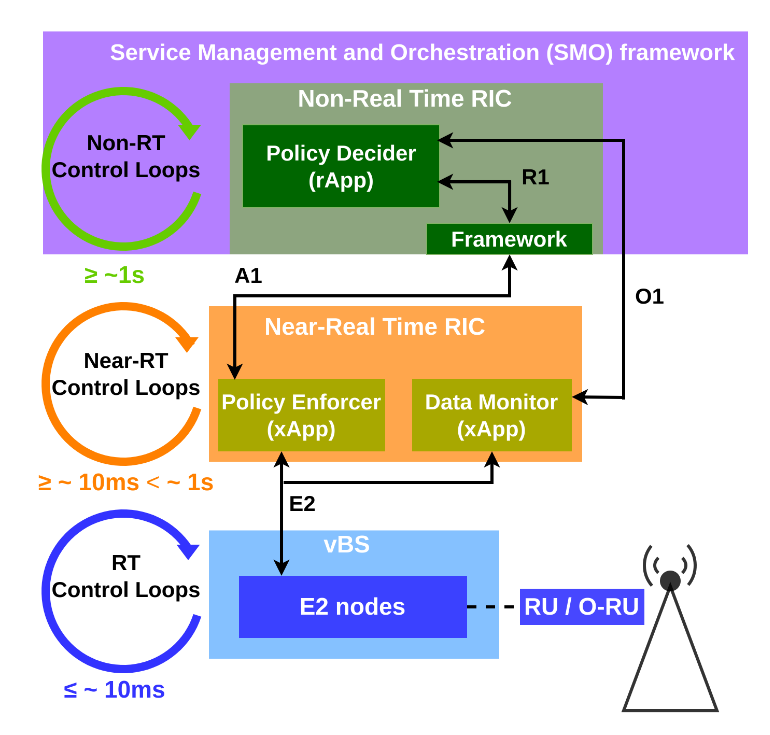
  1. 구성 요소1 : Non-RT RIC의 rApp · 내부에 instantiated rApp으로 정책 결정자(Policy Decider, PD)가 구현되어 있음.
    · PD는 효율적인 policy를 선택하는 algorithm을 구현함.
    · 선택된 policy를 통해 real-time scheduler가 vBS의 운영을 조절함.

  2. 구성 요소2 : Near-RT RIC의 xApp
    · 정책 시행자(Policy Enforcer, PE)
    · PD가 결정한 정책을 실제 E2 Nodes에 전달하고 적용함.

  3. Policy 전달 경로
    · PD는 policy를 결정한 뒤 R1 interface를 통해 Non-RT RIC Framework에 전달.
    · Non-RT RIC Framework는 policy를 A1 interface를 통해 Near-RT RIC으로 전달.
    · Near-RT RIC의 xApp은 전달받은 policy를 E2 interface를 통해 E2 Nodes에 전달.
    · rApp,PD —(R1)—> Non-RT Framework —(A1)—> Near-RT RIC(xApp, PE) —(E2)—> E2Node(RU)
    · optimal policy는 network condition, load에 따라 달라짐. (policy가 선택될 때 해당 조건이 고려되는 것은 아님)

  4. Policy 결정 과정
    · 앞으로의 네트워크 상태나 사용자 부하가 확실치 않은 상황에서 policy를 결정해야하기 때문에 policy는 주기적으로 재평가되어 교체될 수 있음.
    · 각 결정 주기(t)가 끝나면, Near-RT RIC의 data monitor가 E2Node가 수집한 performance와 energy cost metric을 E2 interface를 통해 받아 reward를 계산하고, 이 값을 O1 interface를 통해 PD에 전달한 후 PD는 reward를 기반으로 policy를 선택함.
    · E2Node —(E2)—(metric)—> xApp(data monitor),reward 계산 —(O1)—> rApp,PD
    · O1 interface를 통해 전달된 reward를 기반으로 PD는 더 개선된 정책을 내놓을 수 있도록 학습함.

  5. Policy 결정 순환 구조 · 정책 결정(Non-RT RIC) → 정책 적용(Near-RT RIC → E2 노드) → 결과 측정(Near-RT RIC) → 보상 전달(O1) → 정책 개선(Non-RT RIC)

  6. Non-RT RIC의 구성 - [O-RAN.WG2.Non-RT-RIC-ARCH-R003-v03.00]
    –> Non-RT RIC은 framework와 rApp 총 2가지로 구성됨.

    • Non-RT RIC Framework
      · RAN의 비실시간 control 및 optimization 담당.
      · A1 interface를 통해 Near-RT RIC에 policy와 intelligence info를 제공.
      · AI/ML 모델의 관리 및 workflow를 지원.(training, update…)
      · R1 interface를 통해 rApp에 다양한 service를 노출.(data management, identification…)
      · 아래 그림에서도 A1, R1 interface가 연결된 것을 확인할 수 있음.

    • Non-RT RIC rApps
      · rApp은 framework를 활용하여 RAN 운영과 최적화에 필요한 다음과 같은 service를 제공.
      · radio resource management, data analytics, providing enrichment information

–> 즉, framework는 network 전반적인 계획 및 최적화를 수행하며, rApps는 이를 기반으로 구체적인 서비스를 실행하는 구조인 것 같다.
–> O1 interface는 SMO가 다양한 구성 요소를 관리하기 위한 것이기 때문에 CU, DU, RU 뿐만 아니라 near-RT RIC과도 연결될 수 있는 거였구나.




vBS Control

· O-RAN 규격과 같이 network에 적용되는 policy는 각 시간 slot마다 정해짐.
· 이를 network가 시간 단위로 동작하는 시스템 운영 방식이라고 하더라.
· policy에는 vBS performance에 중요한 scheduling control의 thresholds가 포함되며 다음과 같은 요소들이 있고, policy는 이들의 곱으로 이루어짐.

  • DL Control 변수 집합

$x^d_t \in P_d \times \mathcal{M}_d \times A_d$

· TPC(transmission power control) : $P_d = \lbrace p^d_i, \forall i \in [H] \rbrace$
· MCS(Modulation and Coding Scheme) : $\mathcal{M}_d = \lbrace m^d_i, \forall i \in [I] \rbrace$
· duty cycly(maximum vBS transmission airtime) : $A_d = \lbrace a^d_i, \forall i \in [J] \rbrace$

  • UL Control 변수 집합

$ x^u_t \in \mathcal{M}_u \times A_u $

· MCS : $ \mathcal{M}_u = \lbrace m^u_i, \forall i \in [K] \rbrace $
· airtime : $ A_u = \lbrace a^u_i, \forall i \in [L] \rbrace $

  • RADIO POLICY
    DL contorl과 UL control을 모두 고려하면 다음과 같이 2가지 방법으로 policy를 나타낼 수 있다.

$\mathcal{X} = P_d \times \mathcal{M}_d \times A_d \times \mathcal{M}_u \times A_u.$

$\qquad x_t = (x^d_t, x^u_t) \in \mathcal{X}.$


Reward & Cost

  • policy 목표 1. DL과 UL의 throughput($U_t(x_t)$) 최대화 - [6]
\[U_t(x_t) = \log \left( 1 + \frac{R^d_t(x^d_t)}{d^d_t} \right) + \log \left( 1 + \frac{R^u_t(x^u_t)}{d^u_t} \right)\]

· $R^d_t(x^d_t)$ : 시간 slot t 동안 DL에서 전송된 데이터 양
· $R^u_t(x^u_t)$ : 시간 slot t 동안 UL에서 전송된 데이터 양
· ${d^d_t}$ : 시간 slot t에서 DL backlog (user의 data 소비)
· ${d^u_t}$ : 시간 slot t에서 UL backlog (user의 data upload)
· 각 방향(DL, UL)에서 전송된 데이터 양을 사용자가 요청한 데이터 양으로 나누어 비율을 구한 후, 그 값에 로그를 취해 합산.
· 각각의 항이 자원이 요구량에 대해서 얼마나 효과적으로 사용되는지를 나타내기 때문에, throughput을 의미할 수 있음.
· $d^d_t > 0$, $d^u_t > 0$일 때 해당 함수를 적용하고, 그렇지 않으면 $U_t(x_t)=0$인데, 이는 사용자가 요청한 data가 존재할 때만 네트워크 성능을 측정하겠다는 의미임.

  • policy 목표 2. vBS의 energy cost($P_t(x_t)$) 최소화 - [5]

· $P_t(x_t)$ = BBU(CPU) + RU 고려
· CPU의 전력 소비는 BBU에서 소비되는 전체 전력 중 가장 큰 비중을 차지.
· RU의 전력 소비는 BBU에 있는 DU가 RU와 같은 파워를 하는지에 따라 다를 수 있음.
· $P_t(\cdot)$ (black box modeling)를 통해 vBS의 energy cost를 모델링함.
· black box는 시스템이 너무 복잡한 경우에 내부 메커니즘을 분석하지 않고 입력과 출력만을 기반으로 modeling하는 방법으로, vBS의 전력 소비는 매우 다양한 요인의 영향을 받기 때문에 runtime에서 관찰된 data만을 이용해 modeling함.

  • PD reward function ($\tilde{f}_t: \mathcal{X} \rightarrow \mathbb{R}$)

$\tilde{f}_t(x_t) = U_t(x_t) - \delta P_t(x_t)$

· policy의 2가지 목표를 기반으로 생성된 policy를 집행하는 PD의 성능을 나타내는 지표로, 네트워크 성능을 나타내는 $U_t(x_t)$와 에너지 소비를 나타내는 $P_t(x_t)$ 간의 균형을 맞추는 reward function임.
· $\delta$ 값은 네트워크 성능과 에너지 소비의 상대적 중요도를 조정하는 변수.

  • PD reward function –> normalization ($f_t: \mathcal{X} \rightarrow [0, 1]$)

    \[f_t(x_t) = \frac{\tilde{f}_t(x_t) - \tilde{f}_{\min}}{\tilde{f}_{\max} - \tilde{f}_{\min}}\]

· learning algorithm이 [0,1] 구간에서 작동하기 때문에 정규화를 도입했으며 위의 수식은 정규화를 보장함.


Environment & System Volatility

reward component(policy의 목표들)는 시간에 따라 변동하는데, 이유는 다음과 같음.

· 첫째, small cell network에서 빈번한 user의 traffic 변화(접속, 끊김)으로 인해 user 수, 데이터 사용량이 빠르게 변화함. 그 결과, user traffic이 결정 짓는 $U_t$값이 시간에 따라 변동할 수 있음.

· 둘째, small cell network에서는 네트워크 품질이 빠르게 변화하며, 이는 데이터 전송에도 영향을 미친다. 그 결과, 고정된 $x_t$에서도 $U_t$가 변할 수 있고, 에너지 비용 $P_t$에도 영향을 미침.(SNR이 낮으면 더 많은 BBU 처리 비용을 초래함)

· 셋째, vBS가 운영되는 플랫폼에서 다른 서비스나 네트워크 장치들과 자원을 공유하는 경우에 운영 비용에 영향을 줄 수 있음.

즉! 이러한 모든 요소가 각 스케줄링 기간 t의 시작 시점(slot의 시작 시점)에서는 알 수 없음. 사용자의 부하, 에너지 가용성, 채널 상태 등을 예측하기는 어렵기 때문에, 주기적으로 $x_t$를 결정할 때 $f_t$함수에 대한 접근이 불가능함.

Learning Objective -> PD(정책 결정)의 목표

· PD의 목표 : 어떤 configuration($\lbrace x_t \rbrace _{t=1}^T$)이 주어졌을 때, 시간이 지나면서 가장 이상적인 구성을 점점 더 잘 따라가게 되는 policy를 찾는 것.
· 사용하는 지표 : static expected regret
· regret = 최적의 보상 - 실제 보상

\[R_T = \max_{x \in X} \left( \sum_{t=1}^T f_t(x) \right) - \mathbb{E}\left[ \sum_{t=1}^T f_t(x_t) \right]\]

1번째 항(최적의 보상)
미래를 모두 안다고 가정했을 때, 가장 보상이 높은 configuration을 매번 선택했을 때의 누적 보상.
모든 가능한 구성 x_t 중에서 시간 T까지 누적보상이 가장 큰 것을 선택했을 때의 총 보상.

2번재 항(실제 보상)
실제로 우리가 선택한 구성 $\lbrace x_t \rbrace _{t=1}^T$을 통해 얻은 총 보상.
이 때 선택된 구성은 policy에 의해 선택되었으며, policy에 의해 결정된 구성 선택의 randomrization 가능성에 의해 기대값이 계산됨.

· 최종 목표 : regret의 평균을 0에 수렴시키는 것.

\[\lim_{T \to \infty} \frac{R_T}{T} = 0\]

이를 위해 평균적인 regret이 0에 가까워지도록 만들어야함. 즉, policy가 선택할 구성들이 미래의 보상을 전혀 모르는 상태에서 미래를 다 아는 것 처럼 잘 선택되도록 만들어야함.

왜 이런 policy를 설계했는가??? -> small cell network는 무선환경이고, 사용자 변동이 많고, 불확실성과 변동성을 지닌 상황이기 때문에 미래를 몰라도 점점 더 나은 선택을 하도록 설계된 policy의 방법을 선택한 것.

BANDIT LEARNING ALGORITHM

EXP3 (Exponential-weight Algorithm for Exploration and Exploitation)

· 확률론적 맥락에서 Exploration(탐험)/Exploitation(활용) 사이의 균형을 잡기 위한 algorithm
· 탐색 - 새로운 action을 시도 / 탐험 - 현재까지 가장 잘 작동한 action을 선택
· 각 arm에 대한 가중치를 바탕으로 확률 분포를 사용하여 action을 선택
· 이 때, 특정 action에 집중하거나 과도한 탐색을 방지할 수 있음
· 비정적 보상 환경에서도 잘 작동하고, 탐색과 활용 균형을 자동으로 조절하는 장점이 있지만, 보상 분포를 모델링하지 않고 확률 분포만 사용하기 때문에 action 간 연관성을 활용하지 못하고, 탐험률 $\gamma$와 학습률 $\eta$에 민감함이 단점.

  1. 초기화
    · $K$ : action(arm)의 갯수
    · $\gamma$ : 탐험률
    · $w_i{(1)} = 1 \quad (i = 1, 2, \dots, K)$ : 초기 가중치

  2. 확률 계산
    · 매 라운드 $t$에서, 각 행동 $i$를 선택할 확률 $p_i{(t)}$
    · 1번항 : $(1 - \gamma)$는 행동의 경험적 성과에 기반한 확률
    · 2번항 : $\frac{\gamma}{K}$는 탐험의 요소, 행동의 선택 기회를 보장

    \[p_i(t) = (1 - \gamma) \frac{w_i(t)}{\sum_{j=1}^K w_j(t)} + \frac{\gamma}{K}\]

  3. 보상 추정(보상 업데이트)
    · $\hat{r}_i(t)$ : 선택된 행동 $i$의 추정보상(수정된 보상)
    · ${r}_i(t)$ : 선택된 행동 $i$의 실제보상
    · $\frac{1}{p_i(t)}$ : 관측되지 않은 보상을 보정하기 위한 확률 역수

    \[\hat{r}_i(t) = \frac{r_i(t)}{p_i(t)}\]

  4. 가중치 업데이트
    · 선택된 행동의 추정된 보상을 반영하여 업데이트
    · 높은 보상을 얻은 action의 가중치가 증가
    · $\eta$ : 학습률 (업데이트의 민감도 조절)

    \[w_i(t + 1) = w_i(t) \cdot \exp\left(\frac{\eta \cdot \hat{r}_i(t)}{K}\right)\]

EXP3에서 보상 추정이 필요한 이유

· MCTS에서는 각 라운드 마다 1개의 arm을 선택할 수 있는데, 선택한 arm의 보상만 관찰할 수 있고, 선택하지 않은 arm의 보상을 알 수 없음.
· 이 때문에, 확률적 선택의 영향으로 확률이 낮은 arm의 보상 관측이 제대로 이루어지지 않을 수 있음.
· 선택 확률이 높은 action만 보상 관측이 이루어지는 것을 방지하기 위해 확률의 역수를 곱한 값을 가중치 업데이트에 사용함.
· 확률이 낮은 action의 보상에 확률의 역수를 곱하면 수정된 보상 값은 전보다 커져 확률이 낮은 action의 가중치를 어느정도 보정할 수 있음.

EXP3 in paper

PD Algorithm : 현재 시스템에서 사용하는 normalization reward function $f_t (t = 1, \dots, T)$에 대해서 어떠한 가정도 하지 않는 Exp3 algorithm 사용.

  1. PD의 Algorithm
    · Exp3(Exponential-weight algorithm for Exploration and Exploitation)
    · exploration과 exploitation을 균형있게 조합해 최적의 선택을 찾아감.
    · 환경이나 보상 구조의 변화에 영향 받지 않고 non-stationary 조건에서도 안정적인 성능을 보장.
    · 모든 상황에서 성능 경계가 보장(최악의 경우에서도 일정 수준 이상의 성능을 달성할 수 있다는 의미)
    · normalization reward function의 sequence : $f_t (t = 1, \dots, T)$
    · 해당 algorithm은 bandit feedback을 따름

  2. Bandit feedback
    · bandit feedback이란, 모든 가능한 configuration의 전체적인 보상을 확인할 수 없고 선택된 configuration의 보상만 관찰할 수 있다는 제약을 의미함.
    · 즉, 전체 $f_t(\cdot)$은 알려져 있지 않고, 선택된 configuration $x_t$의 결과 $f_t(x_t)$를 관찰할 수 있음을 의미.
    · 이는 실제 시스템에서 모든 configuration을 테스트하기 어렵기 때문에 사용하는 방법.

  3. 확률 분포 $\lbrace y_t \rbrace$의 학습
    · 각 주기 $t$에서 올바른 확률 분포 $y_t$를 실시간으로 학습.
    · $ \frac{\gamma}{|X|}$ : 탐색 (configuration을 무작위로 선택)
    · $(1-\gamma)$ : 활용 (과거 데이터 기반 좋은 configuration을 선택)
    · $\gamma \in [0,1]$을 통해 탐색과 활용의 균형을 조절

    \[x_t \sim P(x_t = x') = y_t(x'), \quad \forall x' \in X.\] \[Y = \left\{ y \in [0,1]^{|X|} \mid \sum_{x \in X} y(x) = 1 \right\}\] \[y_t(x) = \frac{\gamma}{|X|} + (1 - \gamma) \frac{w_t(x)}{\sum_{x'} w_t(x')}, \quad \forall x \in X.\]

  4. 가중치 $w_t(x)$
    · 각 주기 t의 끝에서 지수 업데이트를 사용하여 가중치를 갱신.

    \[w_{t+1}(x) = w_t(x) \exp\left(-\frac{\gamma \Phi_t(x)}{|X|}\right), \quad \forall x \in X.\]

  5. 비편향 추정치 $\Phi_t(x)$
    · $\Phi_t(x)$ : 비편향 함수 추정치로, 관측되지 않은 보상을 보완하기 관찰된 보상에 확률의 역수를 곱한 값.
    · 시간 t에 configuration $x_t$를 선택했을 때 관찰된 보상 $f_t(x_t)$를 선택 확률 $y_t$로 나눈 값.
    · 선택된 보상만 추정
    · 선택확률로 각 보상값을 가중치화함으로써, 확률이 낮은 configuration도 탐색할 수 있음
    · 3번째 식을 통해 2번째 식이 항상 성립함을 알 수 있음.

    \[\Phi_t(x) = \begin{cases} \frac{f_t(x_t)}{y_t(x_t)}, & \text{if } x = x_t, \\ 0, & \text{otherwise}. \end{cases}\] \[\mathbb{E}[\Phi_t(x) \mid x_1, x_2, \dots, x_{t-1}] = f_t(x_t).\] \[\mathbb{E}[\Phi_t(x_t)] = y_t(x_t) \cdot \frac{f_t(x_t)}{y_t(x_t)} = f_t(x_t).\]

  6. 기대 후회 (Expected Regret, $R_T$)
    · algorithm의 성능을 평가하기 위한 방법으로, $R_T$는 앞서 언급한 것과 같이 알고리즘이 얻은 보상과 최적의 설정이 얻은 보상 간의 차이를 의미.
    · $R_T$는 아래 식에서 볼 수 있듯이, T가 길어질 수록 regret이 줄어드는 “sublinear” 특성을 지님
    · sublinear는 시간이 지남에 따라 최적의 설정을 점점 더 잘 선택한다는 것을 보장함을 의미하며, 시간이 지날 수록 후회가 0에 가까워짐
    · $T$ : 실행된 총 시간
    · $|X|$ : 가능한 설정의 수 (특정 설정 = 특정 policy를 의미할 수 있음)

    \[R_T \leq 2\sqrt{(e - 1)T|X| \ln |X|}\]

  7. meta policy · 개별 정책은 특정 상황에서 시스템이 수행할 구체적인 행동을 정의하는 단일 정책으로 단일 목적이나 단일 변수를 최적화하기 위해 설계
    · 메타 정책은 여러개 개별 정책을 조합하거나 종합적인 기준으로 관리하는 상위 수준의 정책이고 전체 시스템의 최적화를 목표로 함.
    · 위의 기대 후회 공식에서 후회 $R_T$ 값이 $|X|$(meta policy)의 제곱근에 비례함.
    · RT O-RAN 레벨에서는 개별 정책보다 meta policy의 수가 더 작기 때문에 알고리즘이 학습해야할 대상의 수가 줄어들기 때문에 후회도 줄어듦
    · 이 말이 무슨 말을 의미하는지 잘 모르겠다.

PERFORMANCE EVALUATION

실험방법

이전 연구와의 차이가

Algorithm 평가

결론

태그:

카테고리:

업데이트: